Materi Vektor: Definisi, Sifat, Komponen, dan Operasinya

Beberapa dari kalian pasti tidak asing dengan tampilan game Angry Birds di bawah ini. Dalam game tersebut, ketika kita hendak melontarkan burung menggunakan ketapel maka akan muncul garis bantu putus-putus yang menunjukkan jalur lintasan yang akan dilalui burung tersebut.

Jalur lintasan tersebut dinamakan vektor.

Definisi Vektor

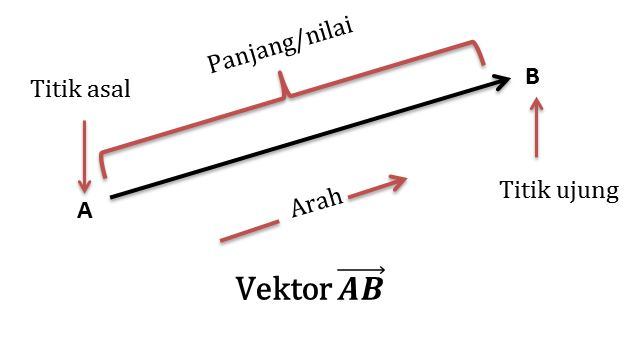
Vektor adalah suatu besaran yang memiliki nilai dan arah. Vektor biasanya digambarkan sebagai sebuah anak panah yang memiliki pangkal dan ujung serta menunjuk ke suatu arah.

Panjang dari panah tersebut dinamakan besar vektor sedangkan arahnya biasa dinyatakan oleh sudut.

Notasi Vektor

Vektor biasanya dinotasikan dengan menambahkan tanda panah di atas huruf. Namun, ada beberapa cara untuk menotasikan vektor, di antaranya:

• Vektor dapat dinotasikan dengan dua huruf kapital atau satu huruf yang di atasnya diberi tanda anak panah. Misalnya: \(\vec{AB}\) atau \(\vec{a}\).
• Vektor dapat dinotasikan dengan dua huruf kapital atau satu huruf yang ditebalkan. Misalnya \(\mathbf{AB}\) atau \(\mathbf{a}\).

Sifat Vektor

Vektor memiliki beberapa sifat umum yang tergantung dari arah vektornya. Beberapa sifat vektor di antaranya:

• Dua vektor dikatakan sama jika keduanya mempunyai nilai dan arah yang sama.
• Vektor negatif mempunyai nilai yang sama besar namun arahnya berlawanan dengan suatu vektor.
• Dua vektor dikatakan sejajar apabila memiliki arah yang sama atau berlawanan arah.

Komponen Vektor

Selain dapat digambarkan dengan anak panah yang menunjukkan besar dan arah, vektor juga dapat diuraikan dalam komponen-komponen pembentuknya.

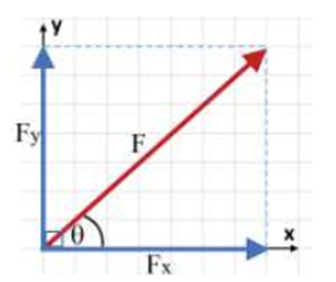
Sebuah vektor dalam ruang dua dimensi dapat diuraikan menjadi dua buah vektor yang saling tegak lurus. Vektor dapat diuraikan menjadi dua komponen, yaitu komponen pada sumbu x (horizontal) dan komponen pada sumbu y (vertikal).

Vektor dalam Kartesian

Suatu vektor \(\vec{a}\) dalam sistem koordinat kartesius dua dimensi dapat dituliskan sebagai berikut:
$$ \vec{a} = a_x \mathbf{i} + a_y \mathbf{j $$
dimana \(a_x\) melambangkan nilai komponen dari vektor \(\vec{a}\) pada arah horizontal, sedangkan \(a_y\) melambangkan nilai komponen dari vektor \(\vec{a}\) pada arah vertikal. Notasi \(\mathbf{i}\) dan \(\mathbf{j}\) merupakan vektor satuan dalam arah horizontal dan vertikal.

Apabila vektor \(\vec{a}$$ berada dalam koordinat tiga dimensi, maka berlaku:
$$ \vec{a} = a_x \mathbf{i} + a_y \mathbf{j} + a_z \mathbf{k} $$
dimana \(\mathbf{i}, \mathbf{j},\) dan \(\mathbf{k}\) merupakan vektor satuan dalam arah sumbu x, sumbu y, dan sumbu z.

Mari kita coba uraikan komponen vektor pada gambar di bawah:

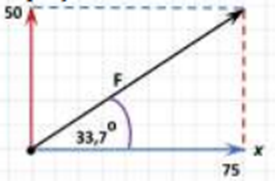
Pada gambar di atas, vektor \(\vec{F}\) memiliki nilai 75 pada komponen horizontal (sumbu x) dan nilai 50 pada komponen vertikal (sumbu y), oleh karena itu vektor \(\vec{F}\) dapat dituliskan sebagai berikut:
$$ \vec{F} = 75 \mathbf{i} + 50 \mathbf{j} $$

Vektor dalam Trigonometri

Apabila panjang vektor membentuk suatu sudut \(\theta\) maka komponen vektornya dapat dituliskan dengan aturan trigonometri. Perhatikan gambar vektor di bawah ini:

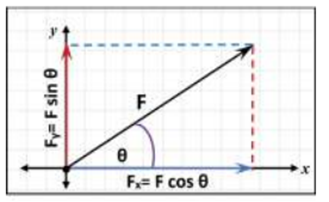
Pada gambar di atas menunjukkan adanya sudut yang dibentuk oleh vektor \(\vec{F}\) pada arah horizontal (sumbu x). Maka besarnya komponen dari vektor \(\vec{F}\) dapat dinyatakan sesuai dengan aturan trigonometri, yaitu:

• Komponen vektor pada arah horizontal (sumbu x) dinyatakan sebagai:
  $$ F_x = F \cos \theta $$
• Komponen vektor pada arah vertikal (sumbu y) dinyatakan sebagai:
  $$ F_y = F \sin \theta $$

Penjumlahan dan Pengurangan Vektor

Hasil dari penjumlahan dan pengurangan vektor dinamakan resultan vektor. Penjumlahan dan pengurangan vektor dilakukan dengan berbagai metode seperti metode grafis, analitis, cosinus, dan sinus.

Penjumlahan dan Pengurangan Vektor Metode Grafis

Pada penjumlahan dan pengurangan vektor metode grafis biasanya menggunakan penggaris dan busur untuk menentukan resultan vektornya, yaitu dengan menggambar vektor secara manual. Terdapat 3 jenis metode yang bisa digunakan, yaitu:

• Metode Segitiga: Metode penjumlahan untuk dua vektor, dilakukan dengan menghubungkan ujung vektor pertama dengan pangkal vektor kedua. Resultan vektor diperoleh dengan menarik panah dari pangkal vektor pertama ke ujung vektor kedua.

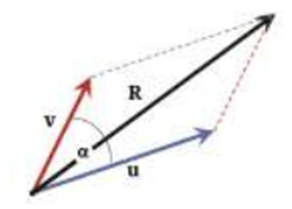
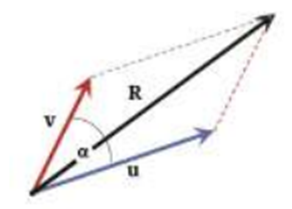
• Metode Jajargenjang: Metode penjumlahan dua vektor, dilakukan dengan mempertemukan dua pangkal vektor pada satu titik kemudian menarik panah dari titik tersebut ke proyeksi dari masing-masing vektor.

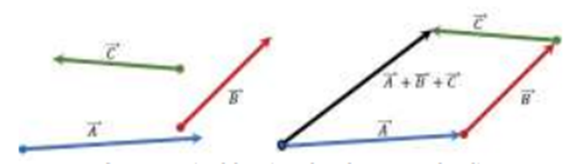
• Metode Poligon: Metode penjumlahan lebih dari dua vektor, prinsip perhitungan resultan vektornya sama seperti metode segitiga.

Resultan Vektor Nol

Vektor nol adalah vektor yang pangkal dan ujung vektornya berhimpit. Vektor nol mempunyai panjang nol dan arahnya tidak tentu.

Penjumlahan dan Pengurangan Vektor Metode Analitis

Menentukan resultan vektor menggunakan metode analitis memerlukan pemahaman terkait trigonometri. Perhatikan gambar di bawah ini:

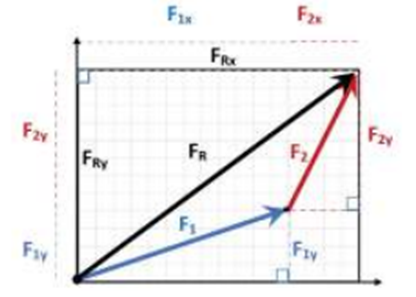
Seperti yang kita ketahui sebelumnya, besarnya tiap komponen pada sumbu x dan y diberikan oleh persamaan:
$$ F_x = F \cos \theta $$
$$ F_y = F \sin \theta $$
Sedangkan untuk total resultan pada masing-masing sumbu jika terdapat lebih dari dua vektor dapat dituliskan sebagai berikut:
$$ F_{Rx} = \sum F_x = F_{1x} + F_{2x} + … $$
$$ F_{Ry} = \sum F_y = F_{1y} + F_{2y} + … $$
Besar resultan vektor total dapat dihitung menggunakan persamaan:
$$ F_R = \sqrt{F_{Rx}^2 + F_{Ry}^2} $$
Sedangkan arah resultannya adalah:
$$ \tan \theta = \frac{F_y}{F_x} $$

Penjumlahan dan Pengurangan Vektor Metode Kosinus

Persamaan kosinus biasanya digunakan untuk menghitung resultan vektor dari dua vektor yang membentuk sudut apit (\alpha\) (seperti pada gambar 7). Besarnya resultan vektor dapat dihitung menggunakan persamaan:
$$ F_R = \sqrt{F_1^2 + F_2^2 + 2F_1F_2 \cos \alpha} $$
Dimana \(F_R$$ adalah resultan total dari dua vektor, \(F_1\) adalah besar dari vektor pertama, \(F_2\) adalah besar vektor kedua, dan\(\alpha\) adalah sudut apit antara dua vektor.

Penjumlahan dan Pengurangan Vektor Metode Sinus

Jika metode kosinus digunakan untuk menentukan resultan vektor dari dua vektor, maka metode sinus digunakan untuk menentukan arah dari resultan vektor yang dihasilkan.

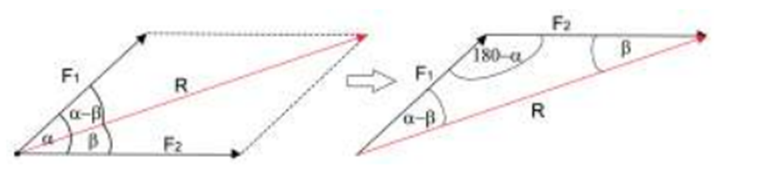
Secara matematis, untuk menentukan arah resultan gaya menggunakan metode sinus dapat dituliskan sebagai berikut:
$$ \sin \beta = \frac{F_1}{R} \sin \alpha $$

Perkalian Vektor

Secara umum perkalian vektor dapat dibedakan menjadi dua jenis yaitu perkalian titik (dot product) dan perkalian silang (cross product).

• Perkalian titik (dot product) merupakan perkalian dari dua vektor yang menghasilkan besaran skalar (nilai saja) sedangkan perkalian silang (cross product) dari dua vektor akan menghasilkan besaran vektor kembali (nilai dan arah).
• Perkalian titik (dot product) menggunakan tanda operasi • sedangkan perkalian silang (cross product) menggunakan tanda operasi ×.

Kesimpulan

Vektor merupakan suatu besaran yang memiliki nilai dan arah. Vektor biasanya dilambangkan dengan anak panah. Vektor yang sama akan mempunyai arah dan besar yang sama.

Vektor negatif mempunyai besar yang sama namun dengan arah berlawanan dengan suatu vektor. Vektor dapat disimbolkan dengan satu atau dua huruf, disimbolkan dengan anak panah di atas hurufnya atau dicetak tebal.

Ada dua cara untuk merepresentasikan vektor, yaitu sebagai anak panah dan yang lainnya menggunakan komponen-komponen dari vektor. Operasi vektor terdiri atas penjumlahan, pengurangan, dan perkalian vektor.