Teori Atom Mekanika Kuantum: Pengertian, Model, Bilangan Kuantum, dan Konfigurasi Elektron

Teori atom mekanika kuantum merupakan salah satu pilar utama dalam fisika modern yang menjelaskan perilaku partikel pada tingkat atom dan subatom.

Teori ini muncul sebagai respons terhadap keterbatasan model atom klasik dalam menjelaskan fenomena yang diamati di tingkat mikroskopis.

Pengertian Teori Atom Mekanika Kuantum

Mekanika kuantum adalah cabang fisika yang mempelajari fenomena yang terjadi pada skala sangat kecil, seperti atom dan partikel subatomik. Berbeda dengan mekanika klasik, yang mengandalkan hukum gerak Newton dan konsep deterministik, mekanika kuantum menggunakan prinsip probabilitas untuk menggambarkan perilaku partikel.

Salah satu konsep fundamental dalam mekanika kuantum adalah dualitas gelombang-partikel, yang menyatakan bahwa partikel, seperti elektron, memiliki sifat sebagai gelombang dan partikel sekaligus.

Teori ini pertama kali dikembangkan pada awal abad ke-20 oleh fisikawan seperti Max Planck, Albert Einstein, Niels Bohr, dan Erwin Schrödinger.

Pemodelan atom dalam mekanika kuantum didasarkan pada prinsip-prinsip matematika yang kompleks, di mana fungsi gelombang (wave function) digunakan untuk menggambarkan keadaan sistem kuantum. Fungsi gelombang ini, dilambangkan dengan Ψ (psi), memberikan informasi tentang probabilitas menemukan partikel dalam posisi tertentu.

Model Atom Berdasarkan Mekanika Kuantum

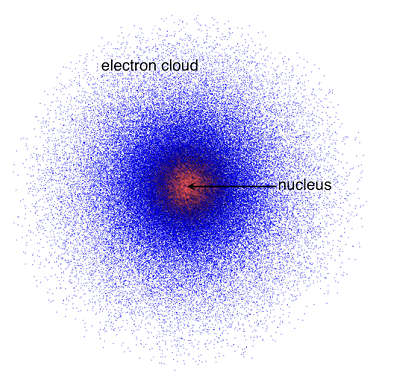
Model atom mekanika kuantum yang paling dikenal adalah model atom Schrödinger, yang mengubah pandangan kita tentang struktur atom. Dalam model ini, elektron tidak lagi dianggap sebagai partikel yang bergerak di jalur tertentu, melainkan sebagai awan probabilitas di sekitar inti atom.

Awan ini menggambarkan kemungkinan lokasi elektron pada suatu waktu tertentu. Dalam konteks ini, elektron memiliki tingkat energi tertentu dan hanya dapat berada pada tingkat energi yang diperbolehkan.

Salah satu persamaan kunci dalam mekanika kuantum adalah Persamaan Schrödinger, yang dituliskan sebagai:

$$ -\frac{\hbar^2}{2m} \nabla^2 \psi + V \psi = E \psi $$

Di mana:

• \( \hbar \) adalah konstanta Planck yang tereduksi,
• \( m \) adalah massa partikel,
• \( \nabla^2 \) adalah operator Laplace,
• \( V \) adalah potensial energi,
• \( E \) adalah energi total, dan
• \( \psi \) adalah fungsi gelombang.

Persamaan ini menggambarkan bagaimana fungsi gelombang berperilaku dalam medan potensial tertentu. Solusi dari persamaan ini memberikan informasi tentang tingkat energi dan bentuk orbit elektron dalam atom.

Bilangan Kuantum

Bilangan kuantum adalah angka yang digunakan untuk mendeskripsikan keadaan dan sifat elektron dalam atom. Ada empat bilangan kuantum utama:

• Bilangan Kuantum Utama ((n)): Menentukan tingkat energi elektron dan jarak rata-rata elektron dari inti atom. Nilai (n) dapat berupa bilangan bulat positif (1, 2, 3,…).
• Bilangan Kuantum Azimuthal ((l)): Menunjukkan bentuk orbital dan nilai momentum sudut elektron. Nilai (l) dapat berkisar dari 0 hingga (n-1). Misalnya, untuk (n = 2), nilai (l) bisa 0 (orbital s) atau 1 (orbital p).
• Bilangan Kuantum Magnetik ((m_l)): Menentukan orientasi orbital dalam ruang. Nilai (m_l) berkisar antara (-l) hingga (+l).
• Bilangan Kuantum Spin ((m_s)): Menunjukkan spin elektron, yang merupakan sifat intrinsik. Nilai (m_s) dapat berupa (-\frac{1}{2}) atau (+\frac{1}{2}).

Bilangan kuantum ini memberikan gambaran yang lengkap tentang keadaan elektron dalam atom dan membantu dalam memahami sifat-sifat kimia dan fisika dari unsur-unsur.

Konfigurasi Elektron

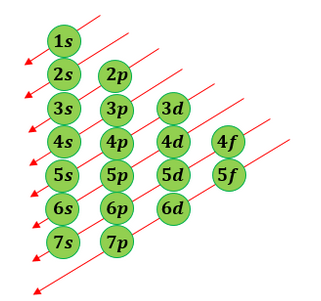
Konfigurasi elektron adalah cara untuk menggambarkan distribusi elektron dalam orbital di sekitar inti atom. Konfigurasi ini mengikuti prinsip-prinsip tertentu, seperti Prinsip Aufbau, yang menyatakan bahwa elektron akan mengisi orbital dengan energi terendah terlebih dahulu.

Contoh konfigurasi elektron untuk atom karbon (C) yang memiliki enam elektron adalah sebagai berikut:

$$ 1s^2 2s^2 2p^2 $$

Konfigurasi ini menunjukkan bahwa dua elektron mengisi orbital 1s, dua elektron lainnya mengisi orbital 2s, dan dua elektron terakhir mengisi orbital 2p. Notasi ini sangat penting dalam memahami sifat-sifat kimia dan ikatan yang dapat dibentuk oleh atom tersebut.

Contoh Lain Konfigurasi Elektron

Berikut adalah beberapa contoh konfigurasi elektron untuk unsur-unsur lain:

• Hidrogen (H): (1s^1)
• Helium (He): (1s^2)
• Neon (Ne): (1s^2 2s^2 2p^6)
• Natrium (Na): (1s^2 2s^2 2p^6 3s^1)
• Klor (Cl): (1s^2 2s^2 2p^6 3s^2 3p^5)

Konfigurasi elektron ini tidak hanya menjelaskan bagaimana elektron terdistribusi, tetapi juga membantu dalam memprediksi sifat-sifat kimia dari unsur-unsur tersebut, seperti reaktivitas, jenis ikatan yang dapat terbentuk, dan banyak lagi.

Pentingnya Teori Atom Mekanika Kuantum

Teori atom mekanika kuantum tidak hanya penting dalam memahami struktur atom, tetapi juga memiliki implikasi yang luas dalam berbagai bidang ilmu pengetahuan dan teknologi. Contohnya, teori ini mendasari pengembangan teknologi modern seperti semikonduktor, laser, dan teknologi informasi.

Selain itu, mekanika kuantum juga berperan dalam bidang kimia kuantum, yang memungkinkan perhitungan yang akurat tentang energi molekul dan reaksi kimia. Hal ini menjadi penting dalam merancang obat-obatan dan material baru, serta dalam pengembangan teknologi energi terbarukan.

Kesimpulan

Teori atom mekanika kuantum memberikan pemahaman yang mendalam tentang struktur atom dan perilaku elektron. Dengan mengubah cara kita melihat partikel subatomik, teori ini memperkenalkan konsep dualitas gelombang-partikel dan probabilitas yang menjadi landasan bagi banyak aspek fisika modern.

Melalui model atom Schrödinger dan bilangan kuantum, kita dapat mendeskripsikan keadaan elektron secara lebih akurat, serta memahami bagaimana elektron terdistribusi dalam orbital yang berbeda. Konfigurasi elektron menjadi kunci untuk menjelaskan sifat-sifat kimia dan reaktivitas unsur-unsur, yang penting dalam banyak aplikasi di bidang sains dan teknologi.

Secara keseluruhan, mekanika kuantum tidak hanya memperkaya pengetahuan kita tentang dunia mikroskopis tetapi juga memberikan dasar bagi banyak inovasi dan penelitian yang terus berlanjut hingga saat ini.

Pengembangan lebih lanjut dalam bidang ini diharapkan akan membuka lebih banyak misteri alam semesta, serta aplikasi baru dalam teknologi yang dapat mempengaruhi kehidupan sehari-hari kita.

Keberhasilan dalam memanfaatkan prinsip-prinsip mekanika kuantum akan menjadi kunci untuk menghadapi tantangan global di masa depan, termasuk dalam bidang kesehatan, energi, dan teknologi informasi.