Rangkaian RLC: Definisi, Karakteristik, Rumus, dan Contoh Soal

Rangkaian RLC merupakan rangkaian listrik yang terdiri dari tiga komponen utama: resistor (R), induktor (L), dan kapasitor (C). Ketiga komponen ini dapat disusun dalam konfigurasi seri atau paralel dan digunakan dalam berbagai aplikasi di bidang teknik elektro dan elektronik.

Rangkaian RLC adalah dasar bagi banyak sistem elektronik dan komunikasi modern, terutama untuk aplikasi seperti filter, osilator, dan penyeimbang sinyal. Untuk menganalisis rangkaian ini, penting untuk memahami interaksi antara arus dan tegangan dalam komponen-komponen tersebut.

• Resistor memberikan hambatan terhadap aliran arus listrik.
• Induktor menyimpan energi dalam bentuk medan magnet.
• Kapasitor menyimpan energi dalam bentuk medan listrik.

Kombinasi ketiga komponen ini menghasilkan respons yang kompleks terhadap sinyal listrik, khususnya sinyal AC (arus bolak-balik).

Karakteristik Resonansi

Rangkaian RLC memiliki karakteristik resonansi, yaitu kemampuan untuk beresonansi pada frekuensi tertentu. Frekuensi resonansi ini sangat penting dalam aplikasi seperti radio, televisi, dan perangkat komunikasi lainnya.

Pada frekuensi resonansi, energi dalam rangkaian berpindah secara efisien antara induktor dan kapasitor, menghasilkan amplitudo arus maksimum.

Komponen Utama dalam Rangkaian RLC

• Resistor (R): Komponen yang membatasi aliran arus listrik. Berdasarkan hukum Ohm, hubungan antara tegangan (V), arus (I), dan resistansi (R) adalah:
  $$ V = I \cdot R $$
  Resistor mengatur laju aliran arus dan mempengaruhi energi yang diserap atau dipancarkan oleh induktor dan kapasitor. Dalam rangkaian AC, resistor tidak mempengaruhi fase antara tegangan dan arus.
• Induktor (L): Komponen yang menyimpan energi dalam bentuk medan magnet. Induktor melawan perubahan arus dengan menghasilkan gaya gerak listrik (GGL) sesuai hukum Lenz:
  $$ V_L = L \frac{dI}{dt} $$
  Induktor mempengaruhi karakteristik frekuensi rangkaian, terutama pada frekuensi resonansi.
• Kapasitor (C): Komponen yang menyimpan energi dalam bentuk medan listrik. Kapasitor menyimpan muatan ketika tegangan diterapkan di antara kedua pelatnya. Hubungan antara muatan (Q), tegangan (V), dan kapasitansi (C) adalah:
  $$ Q = C \cdot V $$
  Kapasitor memungkinkan arus mengalir pada frekuensi tinggi tetapi menghambat pada frekuensi rendah. Reaktansi kapasitif (\(X_C\)) dinyatakan dengan:
  $$ X_C = \frac{1}{2 \pi f C} $$

Rumus-rumus Rangkaian RLC

Rangkaian RLC Seri

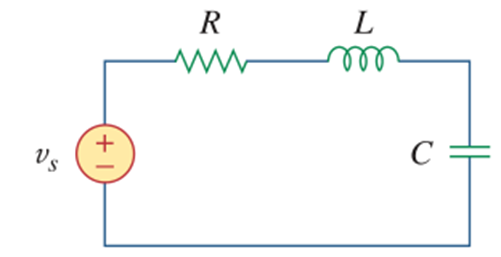
Dalam rangkaian RLC seri, resistor, induktor, dan kapasitor dihubungkan secara berurutan, sehingga arus yang mengalir melalui masing-masing komponen adalah sama. Tegangan total adalah jumlah tegangan di masing-masing komponen:
$$ V_{total} = V_R + V_L + V_C$$

Impedansi total (Z) dari rangkaian RLC seri adalah:
$$ Z = \sqrt{R^2 + (X_L – X_C)^2}$$

di mana:

• \(X_L = \omega L \) adalah reaktansi induktif.
• \( X_C = \frac{1}{\omega C} \) adalah reaktansi kapasitif.

Frekuensi resonansi (\( f_r \)) untuk rangkaian RLC seri adalah:

$$ f_r = \frac{1}{2 \pi \sqrt{L C}}$$

Rangkaian RLC Paralel

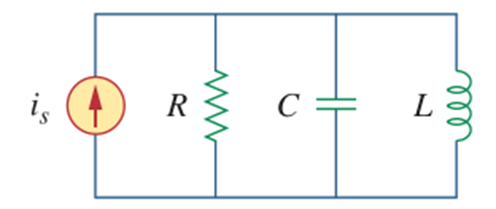
Dalam rangkaian RLC paralel, resistor, induktor, dan kapasitor dihubungkan secara paralel, sehingga tegangan di seluruh komponen adalah sama. Arus total adalah jumlah arus yang mengalir melalui masing-masing komponen:
$$ I_{total} = I_R + I_L + I_C $$

Impedansi total (Z) dari rangkaian RLC paralel adalah:
$$ \frac{1}{Z} = \sqrt{\left(\frac{1}{R}\right)^2 + \left(\frac{1}{X_L} – \frac{1}{X_C}\right)^2} $$

Frekuensi resonansi (( f_r )) untuk rangkaian RLC paralel juga diberikan oleh:
$$ f_r = \frac{1}{2 \pi \sqrt{L C}} $$

Contoh Soal Rangkaian RLC

[Soal 1] Sebuah rangkaian RLC seri terdiri dari resistor 10 Ω, induktor 0,1 H, dan kapasitor 100 µF. Hitung frekuensi resonansi rangkaian tersebut.

Penyelesaian:
Diketahui:
$$ R = 10 \, \Omega $$
$$ L = 0,1 \, H $$
$$ C = 100 \, \mu F = 10^{-4} \, F$$

Frekuensi resonansi (( f_r )):
$$ f_r = \frac{1}{2 \pi \sqrt{L C}} = \frac{1}{2 \pi \sqrt{(0,1 \cdot 10^{-4})}} = 159,15 \, Hz$$

[Soal 2] Dalam sebuah rangkaian RLC paralel, sebuah resistor 50 Ω, induktor 0,2 H, dan kapasitor 10 µF dihubungkan secara paralel. Tentukan impedansi total pada frekuensi 50 Hz.

Penyelesaian:
Diketahui:
$$ R = 50 \, \Omega $$
$$ L = 0,2 \, H $$
$$ C = 10 \, \mu F = 10^{-5} \, F$$
$$ f = 50 \, Hz $$

Reaktansi induktif (\( X_L \)):
$$ X_L = 2 \pi f L = 2 \pi \cdot 50 \cdot 0,2 = 62,83 \, \Omega $$

Reaktansi kapasitif (\( X_C \)):
$$ X_C = \frac{1}{2 \pi f C} = \frac{1}{2 \pi \cdot 50 \cdot 10^{-5}} = 318,31 \, \Omega $$

Impedansi total (Z):
$$ \frac{1}{Z} = \sqrt{\left(\frac{1}{R}\right)^2 + \left(\frac{1}{X_L} – \frac{1}{X_C}\right)^2} = \sqrt{\left(\frac{1}{50}\right)^2 + \left(\frac{1}{62,83} – \frac{1}{318,31}\right)^2} = 47,43 \, \Omega $$

Kesimpulan

Rangkaian RLC menggabungkan resistor, induktor, dan kapasitor yang dapat disusun secara seri atau paralel. Analisis rangkaian ini melibatkan pemahaman tentang bagaimana reaktansi induktif dan kapasitif mempengaruhi arus dan tegangan, terutama pada frekuensi tertentu.

Frekuensi resonansi adalah karakteristik penting dari rangkaian RLC, di mana energi dipertukarkan secara efisien antara induktor dan kapasitor. Pada rangkaian seri, arus adalah sama di seluruh komponen, sementara pada rangkaian paralel, tegangan adalah sama di setiap komponen.

Memahami cara menghitung reaktansi dan impedansi sangat penting untuk merancang dan menganalisis sistem yang menggunakan sinyal AC.