Rangkaian Kapasitor: Rumus, Rangkaian Seri, dan Rangkaian Paralel

Kapasitor adalah komponen listrik yang menyimpan energi dalam bentuk muatan listrik. Mereka memainkan peran penting dalam berbagai aplikasi, mulai dari peralatan elektronik sehari-hari hingga rangkaian listrik yang lebih kompleks.

Memahami bagaimana kapasitor bekerja dalam berbagai konfigurasi, seperti rangkaian seri dan paralel, sangat penting untuk merancang dan menganalisis sirkuit listrik.

Apa Itu Kapasitor?

Sebelum kita masuk ke dalam rumus dan rangkaian, penting untuk memahami konsep dasar kapasitor. Kapasitor adalah perangkat yang terdiri dari dua pelat konduktif yang dipisahkan oleh bahan dielektrik (isolator). Saat tegangan diterapkan di antara pelat-pelat tersebut, kapasitor menyimpan muatan listrik.

Kapasitor biasanya diukur dalam satuan yang disebut Farad (F), dengan kapasitor umum memiliki kapasitansi dalam orde mikrofarad (μF) atau pikofarad (pF).

Rumus Dasar Kapasitor

Untuk menghitung perilaku kapasitor dalam rangkaian listrik, beberapa rumus dasar digunakan:

Kapasitansi (C): Kapasitansi adalah kemampuan kapasitor untuk menyimpan muatan listrik, dan dirumuskan sebagai:
$$ C = \frac{Q}{V} $$
di mana:

• \( C \) adalah kapasitansi dalam Farad,
• \( Q \) adalah muatan dalam Coulomb,
• \( V \) adalah tegangan di antara pelat-pelat kapasitor dalam Volt.

Energi yang Disimpan dalam Kapasitor (E):
$$ E = \frac{1}{2} CV^2 $$
di mana:

• \( E \) adalah energi dalam Joule (terkadang disimbolkan W),
• \( C \) adalah kapasitansi dalam Farad,
• \( V \) adalah tegangan dalam Volt.

Rangkaian Kapasitor Seri

Definisi

Rangkaian seri adalah konfigurasi di mana beberapa kapasitor dihubungkan satu sama lain secara berurutan, sehingga setiap kapasitor berbagi arus yang sama.

Ujung kapasitor pertama terhubung ke sumber tegangan, sedangkan ujung kapasitor terakhir terhubung ke tanah atau titik referensi. Kapasitor yang tersisa dihubungkan di antara kapasitor pertama dan terakhir.

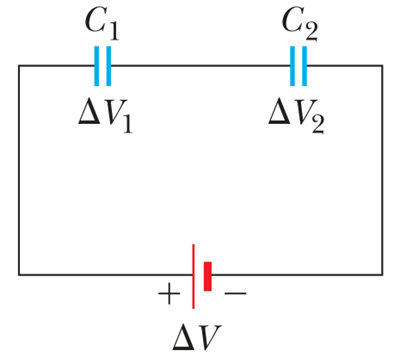
Kapasitansi Total dalam Rangkaian Seri

Dalam rangkaian seri, kapasitansi total \( C_{\text{total}} \) dihitung menggunakan rumus berikut:
$$ \frac{1}{C_{\text{total}}} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} + \ldots + \frac{1}{C_n}$$
di mana \( C_1, C_2, C_3, \ldots, C_n \) adalah kapasitansi individu dari masing-masing kapasitor dalam rangkaian.

Kapasitansi total dalam rangkaian seri selalu lebih kecil dari kapasitansi individu terkecil dalam rangkaian tersebut. Hal ini terjadi karena kapasitor dalam rangkaian seri seolah-olah memperpanjang jarak antara pelat-pelat, sehingga menurunkan kemampuan sistem untuk menyimpan muatan.

Contoh Perhitungan

Misalkan ada tiga kapasitor dalam rangkaian seri dengan nilai 2 μF, 4 μF, dan 6 μF. Kapasitansi total dapat dihitung sebagai berikut:
$$ \frac{1}{C_{\text{total}}} = \frac{1}{2} + \frac{1}{4} + \frac{1}{6} = \frac{6}{12} + \frac{3}{12} + \frac{2}{12} = \frac{11}{12} $$
Maka kapasitansi total adalah:
$$ C_{\text{total}} = \frac{12}{11} \approx 1,09 \, \mu F $$

Tegangan pada Setiap Kapasitor

Tegangan pada setiap kapasitor dalam rangkaian seri tidaklah sama, tetapi jumlah tegangan pada semua kapasitor sama dengan tegangan total yang diterapkan pada rangkaian. Tegangan pada setiap kapasitor \( (V_n) \) diberikan oleh rumus:
$$ V_n = \frac{Q}{C_n} $$
di mana \( Q \) adalah muatan yang disimpan oleh kapasitor (yang sama untuk semua kapasitor dalam rangkaian seri).

Rangkaian Kapasitor Paralel

Definisi

Berbeda dengan rangkaian seri, rangkaian paralel adalah konfigurasi di mana beberapa kapasitor dihubungkan secara paralel satu sama lain.

Dalam konfigurasi ini, setiap kapasitor terhubung langsung ke sumber tegangan, sehingga setiap kapasitor memiliki tegangan yang sama di seluruh terminalnya.

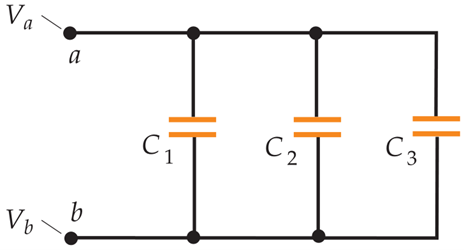
Kapasitansi Total dalam Rangkaian Paralel

Kapasitansi total \( C_{\text{total}} \) dalam rangkaian paralel dihitung dengan menjumlahkan kapasitansi dari setiap kapasitor secara langsung:
$$ C_{\text{total}} = C_1 + C_2 + C_3 + \ldots + C_n $$
di mana:
\( C_1, C_2, C_3, \ldots, C_n \) adalah kapasitansi individu dari masing-masing kapasitor dalam rangkaian.

Kapasitansi total dalam rangkaian paralel selalu lebih besar daripada kapasitansi individu terbesar dalam rangkaian tersebut. Ini terjadi karena kapasitor dalam rangkaian paralel seolah-olah menambah luas pelat-pelat, sehingga meningkatkan kemampuan sistem untuk menyimpan muatan.

Contoh Perhitungan

Misalkan ada tiga kapasitor dalam rangkaian paralel dengan nilai 2 μF, 4 μF, dan 6 μF. Kapasitansi total dalam rangkaian ini adalah:
$$ C_{\text{total}} = 2 + 4 + 6 = 12 \, \mu F $$

Arus pada Setiap Kapasitor

Dalam rangkaian paralel, arus yang melewati setiap kapasitor tidaklah sama, tetapi tegangan pada setiap kapasitor adalah sama dengan tegangan sumber. Arus pada setiap kapasitor dapat dihitung menggunakan rumus:
$$ I_n = C_n \times \frac{dV}{dt} $$
di mana \( I_n \) adalah arus yang mengalir melalui kapasitor \( C_n \), dan \( \frac{dV}{dt} \) adalah laju perubahan tegangan terhadap waktu.

Contoh Penerapan Rangkaian Kapasitor

1. Penggunaan Kapasitor dalam Power Supply

Dalam rangkaian power supply, kapasitor sering digunakan sebagai filter untuk meratakan tegangan setelah proses penyearahan (rectification).

Setelah tegangan AC diubah menjadi DC oleh dioda, tegangan ini masih memiliki riak yang signifikan. Kapasitor digunakan untuk menyimpan muatan dan melepaskannya ketika tegangan turun, sehingga menghasilkan tegangan DC yang lebih halus.

2. Penggunaan Kapasitor dalam Sirkuit Resonansi

Kapasitor juga digunakan dalam sirkuit resonansi, bersama dengan induktor, untuk menghasilkan frekuensi resonansi yang diinginkan. Sirkuit ini digunakan dalam berbagai aplikasi, termasuk radio, komunikasi nirkabel, dan pengolahan sinyal.

Frekuensi resonansi (\( f \)) dari sirkuit LC dapat dihitung dengan rumus:
$$ f = \frac{1}{2\pi\sqrt{LC}} $$
di mana \( L \) adalah induktansi dan \( C \) adalah kapasitansi.

3. Kapasitor dalam Penyimpanan Energi

Kapasitor juga digunakan untuk penyimpanan energi sementara, terutama dalam aplikasi di mana respons cepat diperlukan.

Misalnya, superkapasitor digunakan dalam kendaraan listrik untuk menyediakan daya tambahan selama akselerasi atau untuk menangkap energi regeneratif saat pengereman.

Contoh Soal Rangkaian Kapasitor

Soal 1: Tiga kapasitor dengan kapasitansi masing-masing 4 μF, 6 μF, dan 12 μF dihubungkan secara seri. Hitunglah kapasitansi total dari rangkaian ini.

Pembahasan:
Untuk menghitung kapasitansi total pada rangkaian seri, digunakan rumus:
$$ \frac{1}{C_{\text{total}}} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} = \frac{1}{4} + \frac{1}{6} + \frac{1}{12} = \frac{1}{2} $$
Sehingga:
$$ C_{\text{total}} = \frac{2}{1} = 2 \, \mu F $$

Soal 2: Tiga kapasitor dengan kapasitansi masing-masing 3 μF, 5 μF, dan 7 μF dihubungkan secara paralel. Hitunglah kapasitansi total dari rangkaian ini.

Pembahasan:
Untuk menghitung kapasitansi total pada rangkaian paralel, digunakan rumus:
$$ C_{\text{total}} = C_1 + C_2 + C_3 = 3 + 5 + 7 = 15 \, \mu F $$

Soal 3: Sebuah kapasitor dengan kapasitansi 8 μF dihubungkan ke sumber tegangan 12 V. Hitunglah energi yang disimpan dalam kapasitor tersebut.

Pembahasan:
Energi yang disimpan dalam kapasitor dapat dihitung dengan rumus:
$$ E = \frac{1}{2} CV^2 = \frac{1}{2} \left(8 \times 10^{-6} \, F\right) \left(12^2\right) = 0,576 \, J $$
Jadi, energi yang disimpan dalam kapasitor adalah 0,576 Joule.