Persamaan Arus Bolak-Balik (AC) – Rangkaian, Rumus, dan Contohnya

Arus listrik adalah salah satu konsep dasar dalam fisika dan teknik elektro yang memiliki peran penting dalam kehidupan sehari-hari. Ada dua jenis arus listrik yang dikenal, yaitu arus searah (DC) dan arus bolak-balik (AC).

Pengertian Arus Bolak-balik

Arus bolak-balik atau alternating current (AC) adalah jenis arus listrik di mana arah aliran elektron berubah-ubah secara periodik. Berbeda dengan arus searah (DC) yang mengalir dalam satu arah saja, arus AC berubah arah secara berkala dari positif ke negatif dan sebaliknya. Frekuensi perubahan arah ini disebut frekuensi arus bolak-balik, yang diukur dalam satuan Hertz (Hz).

Di banyak negara, termasuk Indonesia, frekuensi standar untuk arus AC adalah 50 Hz, yang berarti arus tersebut berubah arah sebanyak 50 kali dalam satu detik. Frekuensi yang berbeda digunakan di berbagai negara, seperti 60 Hz yang umum di Amerika Serikat.

Keunggulan utama dari arus AC dibandingkan arus DC adalah kemampuannya untuk ditransmisikan dalam jarak yang jauh dengan kehilangan energi yang lebih sedikit. Ini dimungkinkan berkat penggunaan transformator, yang dapat menaikkan atau menurunkan tegangan arus AC dengan mudah.

Rangkaian Arus Bolak-balik

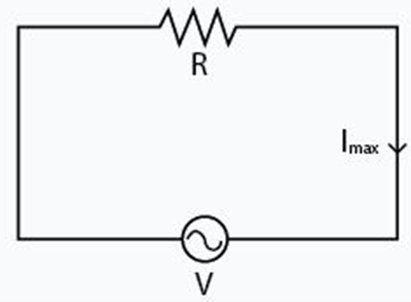
Rangkaian arus bolak-balik adalah susunan komponen listrik yang berfungsi untuk mengalirkan arus AC. Dalam rangkaian ini, kita akan sering menemui tiga komponen utama yaitu resistor, kapasitor, dan induktor. Masing-masing komponen ini memiliki pengaruh yang berbeda terhadap arus AC:

1. Resistor (R): Resistor adalah komponen yang berfungsi untuk menghambat arus listrik, baik dalam rangkaian AC maupun DC. Dalam rangkaian AC, resistor bekerja dengan cara yang sama seperti dalam rangkaian DC, yaitu menurunkan tegangan dan arus berdasarkan hukum Ohm (\(V = IR\)).
2. Kapasitor (C): Kapasitor adalah komponen yang menyimpan energi dalam bentuk medan listrik. Dalam rangkaian AC, kapasitor memiliki sifat yang unik, yaitu menggeser fase arus relatif terhadap tegangan. Hal ini disebabkan oleh sifat kapasitansi yang memungkinkan arus mengalir melalui kapasitor saat tegangan berubah.
3. Induktor (L): Induktor adalah komponen yang menyimpan energi dalam bentuk medan magnet. Seperti kapasitor, induktor juga menggeser fase arus relatif terhadap tegangan, tetapi dalam arah yang berlawanan. Induktansi menyebabkan arus di dalam induktor tertinggal di belakang tegangan.

Ketiga komponen ini dapat disusun dalam berbagai konfigurasi untuk membentuk rangkaian AC yang kompleks, seperti rangkaian seri, paralel, atau kombinasi keduanya. Rangkaian ini banyak digunakan dalam berbagai aplikasi elektronik dan listrik, seperti pada alat-alat rumah tangga, perangkat komunikasi, dan sistem transmisi listrik.

Rumus Persamaan Arus Bolak-balik

Untuk memahami arus bolak-balik secara matematis, kita perlu melihat beberapa rumus dasar yang menggambarkan hubungan antara tegangan, arus, dan elemen-elemen dalam rangkaian AC.

Tegangan dan Arus Sinusoidal

Persamaan Arus dan tegangan dalam rangkaian bolak-balik (AC) biasanya diwakili oleh fungsi sinusoidal sebagai berikut:
$$V(t) = V_m \sin(\omega t + \varphi_v)$$
$$I(t) = I_m \sin(\omega t + \varphi_i)$$
di mana:

• \( V(t) \) dan \( I(t) \) adalah tegangan dan arus sebagai fungsi waktu.
• \( V_m \) dan \( I_m \) adalah nilai puncak (amplitudo) dari tegangan dan arus.
• \( \omega \) adalah kecepatan sudut (rad/s),
• \( \varphi_v \) dan \( \varphi_i \) adalah sudut fase dari tegangan dan arus.

Nilai puncak $$ V_m $$ didefinisikan sebagai:
$$ V_m = \sqrt{2} \cdot V_{rms} $$
di mana \( V_{rms} \) adalah tegangan efektif.

Tegangan Total (\( V_{total} \))

Dalam rangkaian seri AC yang terdiri dari resistor (R), induktor (L), dan kapasitor (C), tegangan total (\( V_{total} \)) dihitung dengan menjumlahkan tegangan-tegangan pada masing-masing komponen secara vektor, karena tegangan pada masing-masing komponen bisa tidak sefasa satu sama lain.

$$ V_{total} = \sqrt{V_R^2 + (V_L – V_C)^2} $$
di mana:

• \( V_R = I \cdot R \) adalah tegangan pada resistor.
• \( V_L = I \cdot X_L \) adalah tegangan pada induktor.
• \( V_C = I \cdot X_C \) adalah tegangan pada kapasitor.

Sedangkan dalam rangkaian paralel AC, tegangan total pada semua cabang rangkaian adalah sama, namun arus pada setiap cabang dapat berbeda. Oleh karena itu, tegangan total pada rangkaian paralel adalah:
$$ V_{total} = V_R = V_L = V_C $$
$$ I_{total} = \sqrt{I_R^2 + (I_L – I_C)^2} $$

Impedansi (Z)

Dalam rangkaian AC, resistansi, kapasitansi, dan induktansi bekerja bersama untuk menentukan impedansi total (Z) rangkaian, yang merupakan hambatan terhadap arus AC. Impedansi dinyatakan sebagai:
$$Z = \sqrt{R^2 + (X_L – X_C)^2}$$
di mana:

• \( R \) adalah resistansi (ohm).
• \( X_L = \omega L \) adalah reaktansi induktif.
• \( X_C = \frac{1}{\omega C} \) adalah reaktansi kapasitif.

Impedansi memiliki satuan ohm (\( \Omega\)) dan menentukan bagaimana arus mengalir melalui rangkaian pada frekuensi tertentu.

Daya dalam Rangkaian AC

Daya dalam rangkaian AC lebih kompleks dibandingkan dengan rangkaian DC karena melibatkan komponen daya nyata, daya reaktif, dan daya semu. Daya nyata (\(P \)) yang dikonsumsi oleh rangkaian dihitung sebagai:
$$ P = V_{rms} \cdot I_{rms} \cdot \cos(\varphi)$$
di mana:

• \( V_{rms} \) dan \( I_{rms} \) adalah nilai efektif tegangan dan arus.
• \( \varphi \) adalah sudut fase antara arus dan tegangan.
• \( \cos(\varphi) \) dikenal sebagai faktor daya.

Sementara itu, daya reaktif (\( Q \)) dihitung sebagai:
$$Q = V_{rms} \cdot I_{rms} \cdot \sin(\varphi)$$

dan daya semu (\( S \)) adalah:
$$ S = V_{rms} \cdot I_{rms} $$
Daya semu dinyatakan dalam volt-ampere (VA), daya nyata dalam watt (W), dan daya reaktif dalam volt-ampere reaktif (VAR).

Contoh Penerapan Arus Bolak-balik

Arus bolak-balik memiliki berbagai penerapan dalam kehidupan sehari-hari, mulai dari penggunaan di rumah tangga hingga sistem industri besar. Beberapa contoh penerapan arus AC adalah:

• Listrik Rumah Tangga: Di rumah, hampir semua peralatan listrik menggunakan arus bolak-balik. Mulai dari lampu, televisi, kulkas, hingga mesin cuci, semuanya dirancang untuk bekerja dengan arus AC. Hal ini karena arus AC lebih efisien untuk didistribusikan melalui jaringan listrik nasional yang melibatkan jarak panjang dari pembangkit listrik ke rumah-rumah.
• Sistem Transportasi Listrik: Kereta api listrik dan sistem transportasi publik lainnya sering menggunakan arus AC karena kemampuannya untuk diubah menjadi tegangan tinggi, yang mengurangi kerugian energi selama transmisi.
• Pembangkit Listrik: Sebagian besar pembangkit listrik, termasuk pembangkit listrik tenaga air, tenaga angin, dan tenaga nuklir, menghasilkan listrik dalam bentuk arus bolak-balik. Pembangkit ini menggunakan generator AC untuk menghasilkan listrik yang kemudian disalurkan melalui jaringan transmisi ke konsumen.
• Pengisian Baterai: Meskipun baterai menyimpan energi dalam bentuk arus searah, pengisian baterai sering melibatkan arus bolak-balik. Charger modern menggunakan penyearah untuk mengubah arus AC dari stopkontak menjadi arus DC yang diperlukan untuk mengisi baterai.
• Penggunaan dalam Industri: Di industri, arus AC digunakan untuk menggerakkan mesin-mesin besar, seperti motor listrik, yang banyak digunakan dalam proses manufaktur. Arus AC juga mendukung operasi perangkat yang memerlukan daya besar, seperti pemanas industri dan pengelasan listrik.

Contoh soal:

1. Tegangan Efektif
   Soal: Sebuah sumber tegangan arus bolak-balik memiliki tegangan maksimum sebesar 311 V. Hitunglah tegangan efektif dari sumber tegangan tersebut.
   
   Jawaban: Gunakan rumus untuk tegangan efektif:
   $$V_{rms} = \frac{V_m}{\sqrt{2}} = 220 \, V$$
   
2. Impedansi Rangkaian
   Soal: Sebuah rangkaian seri terdiri dari sebuah resistor dengan resistansi 50 ohm, induktor dengan reaktansi induktif sebesar 30 ohm, dan kapasitor dengan reaktansi kapasitif sebesar 10 ohm. Hitunglah impedansi total dari rangkaian tersebut.
   
   Jawaban: Gunakan rumus impedansi untuk rangkaian seri:
   $$ Z = \sqrt{R^2 + (X_L – X_C)^2} $$
   $$ Z = \sqrt{50^2 + (30 – 10)^2} = 53.85 \, \Omega $$
   
3. Daya dalam Rangkaian AC
   Soal: Pada sebuah rangkaian AC, arus efektif yang mengalir adalah 5 A dan tegangan efektif adalah 220 V. Jika faktor daya dari rangkaian tersebut adalah 0.8, hitunglah daya aktif yang digunakan oleh rangkaian.
   
   Jawaban: Gunakan rumus daya aktif:
   $$P = V_{rms} \cdot I_{rms} \cdot \cos(\varphi) $$
   $$ P = 220 \cdot 5 \cdot 0.8 = 880 \, W$$

Kesimpulan

Kesimpulannya, arus bolak-balik (AC) adalah jenis arus listrik yang sangat penting dalam kehidupan sehari-hari, terutama dalam distribusi dan penggunaan energi listrik. Dengan kemampuan untuk mengubah arah secara periodik, AC memungkinkan transmisi listrik yang efisien dan fleksibel.

Rangkaian AC yang melibatkan komponen seperti resistor, induktor, dan kapasitor menunjukkan perilaku unik dalam hal arus dan tegangan, yang berbeda dengan rangkaian arus searah (DC). Rumus-rumus yang terkait dengan AC, seperti tegangan efektif, daya, dan impedansi, memberikan dasar pemahaman untuk mengoptimalkan penggunaan AC dalam berbagai aplikasi.

Penerapan arus bolak-balik meliputi hampir semua aspek kehidupan modern, mulai dari listrik rumah tangga, industri, hingga transportasi publik. Dengan fleksibilitasnya untuk diubah menjadi tegangan tinggi atau rendah melalui transformator, AC menjadi pilihan utama dalam sistem distribusi listrik di seluruh dunia.

Pemahaman tentang AC tidak hanya penting untuk ilmu pengetahuan dan teknik, tetapi juga untuk memahami bagaimana energi listrik yang kita gunakan sehari-hari dihasilkan, ditransmisikan, dan dimanfaatkan secara efisien.

Referensi

• Radjawane, M. M., Tinambunan, A.T., dan Jono, S. 2022. Fisika untuk SMA/MA Kelas XII, Jakarta Pusat: Pusat Kurikulum dan Perbukuan Kementerian Pendidikan, Kebudayaan, Riset, dan Teknologi.
• Kumparan.com. Rangkaian arus bolak balik rumus dan contoh soal
• Zenius.net. Arus Bolak-balik – Pengertian, Rumus, dan Contoh Sehari-hari 
• Ilustrasi oleh Unsplash.com