Materi Momentum dan Impuls: Pengertian, Rumus, dan Jenis-Jenisnya

Momentum dan impuls adalah dua konsep penting dalam fisika yang sering digunakan untuk menganalisis pergerakan objek.

Kedua konsep ini sangat berguna dalam memahami bagaimana benda bergerak dan berinteraksi satu sama lain, terutama pada saat terjadi tumbukan atau perubahan kondisi. Dengan memahami momentum dan impuls, kita bisa memprediksi hasil dari berbagai interaksi fisik di lingkungan kita.

Momentum dan impuls adalah dua konsep fisika yang berkaitan erat dan sering kali digunakan untuk menganalisis pergerakan objek, terutama saat terjadi interaksi seperti tumbukan.

Artikel ini akan menguraikan pengertian, rumus, jenis-jenis momentum dan tumbukan, serta penerapan hukum kekekalan momentum dan konsep impuls.

Pengertian Momentum

Momentum adalah besaran fisika yang menggambarkan jumlah gerak yang dimiliki oleh suatu objek. Momentum merupakan hasil kali dari massa dan kecepatan suatu benda. Dalam bahasa sehari-hari, momentum sering dikaitkan dengan kekuatan atau daya dorong benda yang bergerak.

Misalnya, bola yang bergerak dengan kecepatan tinggi akan memiliki momentum lebih besar daripada bola yang bergerak lambat, meskipun keduanya memiliki massa yang sama. Secara matematis, momentum dinyatakan dengan persamaan:

$$ p = m \cdot v $$
dengan:

• \(p\) = momentum (kg·m/s),
• \(m\) = massa benda (kg),
• \(v\) = kecepatan benda (m/s).

Momentum adalah besaran vektor, yang berarti ia memiliki besar dan arah. Arah momentum searah dengan arah kecepatan benda.

Hukum Kekekalan Momentum

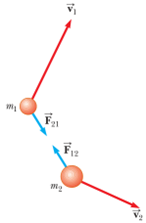
Hukum kekekalan momentum menyatakan bahwa total momentum dalam suatu sistem tertutup (sistem yang tidak dipengaruhi oleh gaya luar) akan tetap konstan, asalkan tidak ada gaya luar yang bekerja pada sistem tersebut.

Artinya, jika dua atau lebih benda berinteraksi (misalnya melalui tumbukan), total momentum sebelum dan setelah interaksi akan sama. Secara matematis, hukum kekekalan momentum dapat dinyatakan sebagai:

$$ p_{sebelum} = p_{sesudah} $$

Atau secara umum, dalam bentuk vektor:

$$ m_1 \cdot v_1 + m_2 \cdot v_2 = m_1 \cdot v_1′ + m_2 \cdot v_2′ $$

Di mana:

• \(m_1\) dan \(m_2\) = massa benda pertama dan kedua,
• \(v_1\) dan \(v_2\) adalah kecepatan awal benda pertama dan kedua,
• \(v_1’\) dan \(v_2’\) adalah kecepatan akhir benda pertama dan kedua.

Hukum ini berlaku dalam semua jenis tumbukan, baik itu tumbukan elastis, tidak elastis, maupun tidak elastis sempurna.

Jenis-Jenis Tumbukan

Tumbukan adalah interaksi antara dua atau lebih benda yang menyebabkan perubahan kecepatan benda-benda tersebut. Berdasarkan konservasi energi dan momentum, tumbukan dapat diklasifikasikan menjadi tiga jenis utama:

Tumbukan Elastis = Tumbukan lenting sempurna

Pada tumbukan elastis, tidak hanya momentum yang kekal, tetapi energi kinetik total sistem juga kekal. Contoh tumbukan elastis terjadi pada bola bilyar yang saling bertabrakan, di mana bola-bola tersebut tidak mengalami perubahan bentuk atau kehilangan energi dalam bentuk lain seperti panas.

Persamaan yang digunakan dalam tumbukan elastis adalah:
$$ m_1 \cdot v_1 + m_2 \cdot v_2 = m_1 \cdot v_1′ + m_2 \cdot v_2′ $$

Dan energi kinetik total sebelum dan sesudah tumbukan adalah sama:
$$ \frac{1}{2} m_1 \cdot (v_1)^2 + \frac{1}{2} m_2 \cdot (v_2)^2 = \frac{1}{2} m_1 \cdot (v_1′)^2 + \frac{1}{2} m_2 \cdot (v_2′)^2 $$

Tumbukan Tidak Elastis = Tumbukan tidak lenting sama sekali

Pada tumbukan tidak elastis, momentum tetap kekal, tetapi sebagian energi kinetik hilang (misalnya dalam bentuk panas, suara, atau deformasi benda). Benda setelah tumbukan mungkin mengalami perubahan bentuk, seperti pada kecelakaan mobil.

Besar momentum tumbukan tidak elestis:

$$ m_1 \cdot v_1 + m_2 \cdot v_2 = m_1 \cdot v_1′ + m_2 \cdot v_2′ $$

Besar energi kinetik tumbukan tidak elestis:

$$ \frac{1}{2} m_1 \cdot v_1^2 + \frac{1}{2} m_2 \cdot v_2^2 > \frac{1}{2} m_1 \cdot (v_1′)^2 + \frac{1}{2} m_2 \cdot (v_2′)^2 $$

Pada tumbukan ini, koefisien restitusi \(e\) (nilai antara 0 dan 1) digunakan untuk menghitung perubahan kecepatan relatif:
$$ e = \frac{v_2′ – v_1′}{v_1 – v_2} $$

Koefisien restitusi \(e\):

• \(e=1\) untuk tumbukan elastis sempurna,
• \(0 < e < 1\) untuk tumbukan elastis sebagian,
• \(e = 0\) untuk tumbukan tidak elastis sempurna.

Tumbukan Tidak Elastis Sempurna = Tumbukan lenting sebagian

Pada tumbukan ini, dua benda yang bertumbukan akan saling menempel dan bergerak bersama-sama setelah tumbukan. Momentum tetap kekal, tetapi energi kinetik yang hilang lebih banyak daripada pada tumbukan tidak elastis biasa.

Besar momentum tumbukan tidak elestis sempurna:

$$ m_1 \cdot v_1 + m_2 \cdot v_2 = m_1 \cdot v_1′ + m_2 \cdot v_2′ $$

Besar energi kinetik tumbukan tidak elestis sempurna:

$$ \frac{1}{2} m_1 \cdot v_1^2 + \frac{1}{2} m_2 \cdot v_2^2 \neq \frac{1}{2} m_1 \cdot (v_1′)^2 + \frac{1}{2} m_2 \cdot (v_2′)^2 $$

Sebagian energi kinetik berubah menjadi bentuk lain seperti panas atau deformasi.

Dengan menggunakan rumus-rumus ini, kita dapat mengkalkulasi pergerakan dan perubahan energi benda setelah berbagai jenis tumbukan.

Penerapan Momentum dan Hukum Kekekalan Momentum

Hukum kekekalan momentum banyak diterapkan dalam kehidupan sehari-hari, terutama dalam bidang mekanika dan teknik. Berikut adalah beberapa contoh penerapannya:

• Kecelakaan Kendaraan: Saat dua mobil bertabrakan, momentum total sebelum dan setelah tabrakan akan tetap konstan, asalkan tidak ada gaya luar yang bekerja. Analisis ini membantu memahami sejauh mana kerusakan yang terjadi dan digunakan dalam rekonstruksi kecelakaan.
• Roket: Prinsip konservasi momentum juga berlaku pada peluncuran roket. Ketika bahan bakar dibakar dan gas dikeluarkan ke belakang roket dengan kecepatan tinggi, momentum ke belakang dari gas akan diimbangi dengan momentum ke depan dari roket, sehingga roket dapat bergerak maju.

Pengertian Impuls

Impuls adalah besaran yang berhubungan dengan perubahan momentum suatu benda. Impuls didefinisikan sebagai hasil kali gaya yang bekerja pada benda dengan selang waktu di mana gaya tersebut bekerja.

Dalam kata lain, impuls adalah cara untuk menggambarkan efek dari gaya yang bekerja selama periode waktu tertentu. Secara matematis, impuls dinyatakan dengan persamaan:

$$ I = F \cdot \Delta t$$
Di mana:

• \(I\) adalah impuls (dalam newton-detik atau N·s),
• \(F\) adalah gaya yang bekerja (dalam newton),
• \(\Delta t\) adalah selang waktu gaya bekerja (dalam detik).

Menurut hukum kedua Newton, impuls juga sama dengan perubahan momentum:

$$I = \Delta p = m \cdot \Delta v$$
Di mana:

• \(\Delta p\) adalah perubahan momentum,
• \(\Delta v\) adalah perubahan kecepatan benda.

Penerapan Impuls

Konsep impuls sering digunakan dalam berbagai situasi di mana gaya bekerja dalam waktu singkat, tetapi menghasilkan perubahan besar pada momentum. Beberapa contoh penerapannya antara lain:

• Olahraga: Dalam olahraga seperti sepak bola, basket, atau tenis, pemain memukul atau menendang bola untuk memberinya kecepatan. Impuls diberikan oleh gaya tendangan atau pukulan yang berlangsung dalam selang waktu singkat, menghasilkan perubahan kecepatan bola.
• Airbag pada Mobil: Airbag dirancang untuk mengurangi gaya yang diterima oleh penumpang selama kecelakaan. Dengan memperpanjang waktu perlambatan, gaya yang diberikan pada tubuh penumpang menjadi lebih kecil, sehingga mengurangi cedera yang mungkin terjadi. Ini adalah contoh nyata penerapan konsep impuls untuk mengurangi dampak kecelakaan.
• Pegas dan Bumper: Impuls juga digunakan dalam desain pegas atau bumper kendaraan yang dirancang untuk menyerap energi selama tabrakan. Dengan mengurangi gaya yang diterima kendaraan, risiko kerusakan dapat diminimalkan.

Kesimpulan

Momentum dan impuls adalah dua konsep fundamental dalam fisika yang memainkan peran penting dalam memahami gerakan dan interaksi benda. Momentum menggambarkan jumlah gerak yang dimiliki oleh suatu benda, sementara impuls menjelaskan bagaimana gaya yang bekerja dalam waktu tertentu dapat mengubah momentum benda tersebut.

Hukum kekekalan momentum, yang menyatakan bahwa total momentum dalam sistem tertutup tetap konstan, sangat penting dalam memahami berbagai fenomena seperti tumbukan elastis dan tidak elastis. Di sisi lain, konsep impuls memungkinkan kita untuk menganalisis bagaimana gaya yang bekerja dalam periode waktu tertentu mempengaruhi kecepatan dan gerakan benda.

Penerapan praktis dari kedua konsep ini dapat ditemukan dalam berbagai situasi sehari-hari, mulai dari olahraga hingga teknologi keselamatan kendaraan, serta dalam mekanika dan teknik pada umumnya. Pemahaman yang baik tentang momentum dan impuls memberikan landasan kuat dalam analisis gerak dan interaksi objek dalam dunia nyata.