Hambatan Jenis: Pengertian, Rumus, Besaran, dan Contoh Soalnya

Dalam bidang fisika, khususnya listrik, hambatan jenis merupakan salah satu konsep penting yang berkaitan dengan sifat-sifat bahan penghantar. Memahami hambatan jenis membantu kita memahami bagaimana bahan-bahan yang berbeda mempengaruhi arus listrik yang mengalir melalui penghantar.

Hambatan jenis memiliki implikasi langsung dalam industri, terutama dalam bidang konstruksi dan manufaktur perangkat elektronik. Dalam aplikasi praktis, pemilihan bahan dengan hambatan jenis yang tepat dapat mengurangi biaya produksi, meningkatkan efisiensi energi, dan memperpanjang umur perangkat.

Selain itu, penelitian tentang hambatan jenis juga berperan penting dalam pengembangan material baru yang memiliki sifat listrik yang diinginkan, seperti peningkatan konduktivitas atau peningkatan isolasi.

Pengertian Hambatan Jenis

Hambatan jenis, atau sering disebut resistivitas (\( \rho \)), adalah ukuran seberapa besar suatu bahan menahan aliran arus listrik. Hambatan jenis ini merupakan sifat intrinsik bahan dan tidak bergantung pada ukuran atau bentuk bahan tersebut, melainkan hanya pada sifat bahan itu sendiri.

Secara umum, hambatan jenis didefinisikan sebagai hambatan yang dimiliki oleh sebuah penghantar per satuan panjang dan luas penampang.

Nilai hambatan jenis yang lebih besar menunjukkan bahwa bahan tersebut lebih sulit dilalui oleh arus listrik, sedangkan nilai hambatan jenis yang lebih kecil berarti bahan tersebut lebih mudah dilalui oleh arus listrik. Hambatan jenis sangat bergantung pada jenis material dan juga temperatur.

Misalnya, logam seperti tembaga dan aluminium memiliki hambatan jenis yang sangat rendah, sehingga keduanya merupakan konduktor yang baik. Di sisi lain, bahan seperti karet atau plastik memiliki hambatan jenis yang sangat tinggi dan dikenal sebagai isolator.

Peran Hambatan Jenis dalam Rangkaian Listrik

Dalam sebuah rangkaian listrik, hambatan jenis berperan penting dalam menentukan seberapa efisien arus listrik dapat mengalir melalui penghantar.

Jika hambatan jenis suatu bahan tinggi, energi listrik lebih banyak akan dihambat dan sebagian energi akan berubah menjadi panas.

Sebaliknya, bahan dengan hambatan jenis rendah akan membiarkan arus listrik mengalir dengan lebih mudah, sehingga energi lebih efisien ditransmisikan.

Rumus Hambatan Jenis

Rumus yang digunakan untuk menghitung hambatan jenis berasal dari hukum Ohm dan hubungan antara hambatan listrik, panjang penghantar, dan luas penampang.

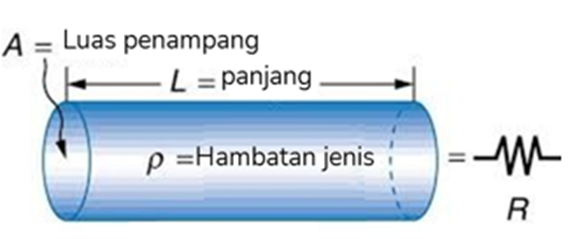
Hambatan listrik (\( R \)) suatu penghantar dihubungkan dengan hambatan jenis (\( \rho \)) melalui persamaan:
$$ R = \rho \times \frac{L}{A} $$
di mana:

• \( R \) adalah hambatan listrik dalam ohm (Ω),
• \( \rho \) adalah hambatan jenis atau resistivitas dalam ohm meter (Ω·m),
• \( L \) adalah panjang penghantar dalam meter (m),
• \( A \) adalah luas penampang penghantar dalam meter persegi (m²).

Dari rumus tersebut, dapat dilihat bahwa hambatan listrik suatu penghantar sebanding dengan panjang penghantar dan berbanding terbalik dengan luas penampang.

Dengan kata lain, semakin panjang penghantar atau semakin kecil luas penampangnya, maka hambatan listrik akan semakin besar. Hambatan jenis memiliki satuan ohm meter (Ω·m) dalam Sistem Internasional (SI).

Nilai hambatan jenis berbeda untuk setiap bahan, dan biasanya dicantumkan dalam tabel material sebagai parameter penting ketika merancang perangkat elektronik atau rangkaian listrik.

Faktor-faktor yang Mempengaruhi Hambatan Jenis

1. Jenis Bahan: Setiap bahan memiliki nilai hambatan jenis yang berbeda. Misalnya, logam seperti tembaga dan perak memiliki hambatan jenis yang sangat rendah, sementara bahan isolator seperti kaca dan karet memiliki hambatan jenis yang sangat tinggi.
2. Temperatur: Hambatan jenis umumnya meningkat dengan bertambahnya temperatur. Pada logam, kenaikan temperatur menyebabkan getaran atom meningkat, yang mengganggu aliran elektron dan meningkatkan hambatan. Namun, beberapa bahan seperti semikonduktor justru memiliki hambatan jenis yang menurun ketika suhunya naik.

Tabel Nilai Hambatan Jenis untuk Bahan-Bahan Umum

Bahan	Hambatan Jenis (Ω·m)
Tembaga	\(1.68 \times 10^{-8}\)
Aluminium	\(2.82 \times 10^{-8}\)
Baja	\(1.0 \times 10^{-7}\)
Karet	\(1.0 \times 10^{13}\)
Kaca	\(1.0 \times 10^{12}\)

Pengaruh Hambatan Jenis dalam Praktik

Dalam praktiknya, hambatan jenis digunakan untuk menentukan material mana yang paling cocok untuk berbagai aplikasi listrik. Misalnya, karena tembaga memiliki hambatan jenis yang rendah, tembaga sering digunakan dalam kabel listrik untuk mengurangi kehilangan energi akibat hambatan.

Sebaliknya, bahan dengan hambatan jenis tinggi seperti karet digunakan sebagai bahan isolator dalam kabel listrik.

Contoh Soal Hambatan Jenis

Berikut adalah beberapa contoh soal mengenai hambatan jenis beserta pembahasannya untuk membantu Anda memahami konsep ini lebih baik.

Contoh Soal 1: Menghitung Hambatan Listrik Berdasarkan Hambatan Jenis
Sebuah kawat tembaga dengan panjang 2 meter dan luas penampang 1 mm² digunakan dalam suatu rangkaian listrik. Jika hambatan jenis tembaga adalah \(1.68 \times 10^{-8}\, (\Omega \cdot m)\), hitunglah hambatan listrik kawat tersebut.

Pembahasan:
Diketahui:

• Panjang kawat \( L = 2\,m \)
• Luas penampang \( A = 1\,mm^2 = 1 \times 10^{-6}\, m^2 \)
• Hambatan jenis tembaga \( \rho = 1.68 \times 10^{-8}\, \Omega \cdot m \)

Menggunakan rumus hambatan listrik:
$$ R = \rho \times \frac{L}{A} = 1.68 \times 10^{-8} \left(\frac{2}{1 \times 10^{-6}}\right) = 0.0336\, \Omega $$

Jadi hambatan listrik kawat tembaga tersebut adalah 0.0336 ohm.

Contoh Soal 2: Menghitung Hambatan Jenis Suatu Bahan
Sebuah kawat dengan panjang 5 meter memiliki hambatan sebesar 10 ohm. Jika luas penampang kawat tersebut adalah 2 mm², hitunglah hambatan jenis bahan kawat tersebut.

Pembahasan:
Diketahui:

• Panjang kawat \( L = 5\,m \)
• Hambatan \( R = 10\, \Omega \)
• Luas penampang \( A = 2\, mm^2 = 2 \times 10^{-6}\, m^2 \)

Menggunakan rumus hambatan listrik:
$$ R = \rho \times \frac{L}{A} $$

Maka, hambatan jenis dapat dihitung dengan:
$$ \rho = \frac{R \times A}{L} = \frac{10 \times (2 \times 10^{-6})}{5} = 4 \times 10^{-6}\, \Omega \cdot m $$

Jadi hambatan jenis bahan kawat tersebut adalah \( 4 \times 10^{-6} \, \Omega \cdot m \).

Contoh Soal 3: Menghitung Panjang Kawat Berdasarkan Hambatan dan Hambatan Jenis
Sebuah kawat aluminium memiliki hambatan sebesar 5 ohm dan luas penampang sebesar 0.5 mm². Jika hambatan jenis aluminium adalah \( 2.82 \times 10^{-8} \, \Omega \cdot m \), hitunglah panjang kawat tersebut.

Pembahasan:
Diketahui:

• Hambatan \( R = 5\, \Omega \)
• Luas penampang \( A = 0.5\, mm^2 = 0.5 \times 10^{-6}\, m^2 \)
• Hambatan jenis aluminium \( \rho = 2.82 \times 10^{-8}\, \Omega \cdot m \)

Menggunakan rumus hambatan listrik:
$$ L = \frac{R \times A}{\rho} = \frac{5 \times (0.5 \times 10^{-6})}{2.82 \times 10^{-8}} = 88.65\, m $$

Jadi panjang kawat aluminium tersebut adalah sekitar 88.65 meter.

Kesimpulan

Hambatan jenis merupakan sifat intrinsik suatu bahan yang menunjukkan seberapa besar bahan tersebut menahan aliran arus listrik. Hambatan jenis tergantung pada jenis bahan dan juga dapat dipengaruhi oleh temperatur. Semakin tinggi hambatan jenis suatu bahan, semakin besar hambatan listrik yang dihasilkan saat arus listrik mengalir melalui bahan tersebut.

Rumus hambatan jenis \( R = \rho \times \frac{L}{A} \) menghubungkan hambatan listrik, panjang penghantar, luas penampang, dan hambatan jenis. Besaran hambatan jenis dinyatakan dalam satuan ohm meter (Ω·m), dan setiap bahan memiliki nilai resistivitas yang berbeda-beda.

Bahan dengan hambatan jenis rendah seperti tembaga dan aluminium digunakan sebagai konduktor, sementara bahan dengan hambatan jenis tinggi seperti karet dan kaca digunakan sebagai isolator.