Materi Gerak Rotasi – Momen Gaya dan Inersia, Rumus dan Contoh Soalnya

Gerak rotasi adalah salah satu konsep fundamental dalam fisika yang menjelaskan perputaran suatu objek di sekitar sumbu tertentu. Dalam fenomena ini, setiap partikel pada objek yang berputar bergerak mengikuti lintasan melingkar dengan sumbu rotasi sebagai pusatnya.

Contoh nyata dari gerak rotasi dapat dilihat pada roda yang berputar, baling-baling kipas angin, atau bahkan planet yang berotasi mengelilingi porosnya.

Gerak rotasi tidak hanya melibatkan pergerakan sederhana tetapi juga melibatkan berbagai besaran fisika yang sangat penting untuk dipahami. Besaran-besaran seperti kecepatan sudut, percepatan sudut, momen gaya (atau torsi), dan momen inersia memainkan peran sentral dalam menentukan bagaimana objek tersebut bergerak atau merespons ketika dikenai gaya dari luar.

Kecepatan sudut menggambarkan seberapa cepat suatu benda berputar dalam satuan waktu, sementara percepatan sudut menunjukkan perubahan kecepatan sudutnya. Momen gaya atau torsi adalah gaya yang menyebabkan perubahan dalam gerak rotasi, dan momen inersia mencerminkan resistansi objek terhadap perubahan dalam gerakan tersebut.

Besaran-besaran ini bekerja bersama-sama untuk menjelaskan dinamika rotasi, sehingga kita dapat memahami bagaimana suatu benda bisa dipercepat atau diperlambat dalam gerak rotasi.

Pengertian Gerak Rotasi

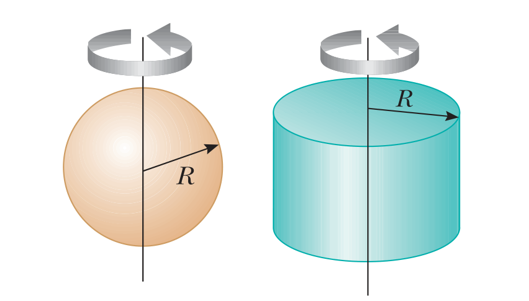
Gerak rotasi terjadi ketika suatu objek berputar di sekitar sumbu tetap. Setiap partikel dalam benda yang berotasi mengikuti lintasan melingkar dengan pusat di sumbu rotasi.

Contoh dari gerak rotasi adalah roda yang berputar, baling-baling kipas angin, atau planet yang berotasi di sekitar porosnya.

Dalam gerak rotasi, besaran-besaran seperti kecepatan sudut, percepatan sudut, momen gaya (torque), dan momen inersia sangat penting. Momen gaya dan momen inersia menentukan bagaimana gerakan rotasi suatu benda berubah saat dikenai gaya luar.

Momen Gaya (Torque)

Pengertian Momen Gaya

Momen gaya, atau yang sering disebut sebagai torsi, adalah gaya yang menyebabkan benda mengalami percepatan sudut atau perubahan dalam gerak rotasi. Momen gaya berbanding lurus dengan besarnya gaya yang diterapkan dan jarak dari titik tumpu tempat gaya tersebut diterapkan.

Secara matematis, momen gaya dinyatakan dengan rumus:
$$ \tau = F \cdot r \cdot \sin(\theta) $$

Di mana:

• \( \tau\) adalah momen gaya (dalam newton-meter atau N·m),
• \( F\) adalah gaya yang diterapkan (dalam newton),
• \( r \) adalah jarak dari sumbu rotasi ke titik tempat gaya diterapkan (dalam meter),
• \( \theta \) adalah sudut antara gaya dan garis dari titik tumpu ke titik penerapan gaya.

Jika gaya tegak lurus dengan jarak \( r \), maka \( \sin(\theta) = 1 \), dan rumusnya menjadi:
$$ \tau = F \cdot r $$

Momen gaya adalah besaran vektor yang arah rotasinya ditentukan oleh aturan tangan kanan: jika jari-jari tangan kanan menunjuk ke arah gaya, maka ibu jari akan menunjuk ke arah rotasi akibat momen gaya tersebut.

Contoh Soal Momen Gaya dan Gerak Rotasi

Soal 1: Sebuah gaya sebesar 50 N diterapkan pada ujung batang sepanjang 2 meter. Gaya tersebut membentuk sudut 90° terhadap batang. Hitung momen gaya yang dihasilkan.

Penyelesaian:
Diketahui:

• \( F = 50 \, \text{N} \)
• \( r = 2 \, \text{m} \)
• \( \theta = 90° \)

Karena \( \theta = 90° \), maka \( \sin(90°) = 1 \).

Maka, momen gaya adalah:
$$ \tau = F \cdot r = 50 \, \text{N} \cdot 2 \, \text{m} = 100 \, \text{N·m} $$

Jadi, momen gaya yang dihasilkan adalah 100 N·m.

Soal 2: Sebuah gaya sebesar 40 N diterapkan pada pintu sepanjang 1,5 meter dari engselnya. Gaya tersebut membentuk sudut 45° dengan pintu. Hitung momen gaya yang dihasilkan.

Penyelesaian:
Diketahui:

• \( F = 40 \, \text{N} \)
• \( r = 1,5 \, \text{m} \)
• \( \theta = 45° \)

Momen gaya adalah:
$$ \tau = F \cdot r \cdot \sin(45°) = 40 \cdot 1,5 \cdot \sin(45°) = 42,42 \, \text{Nm} $$

Jadi, momen gaya yang dihasilkan adalah sekitar 42,42 Nm.

Momen Inersia

Pengertian Momen Inersia

Momen inersia adalah ukuran resistansi suatu benda terhadap perubahan dalam gerak rotasinya. Momen inersia bergantung pada distribusi massa benda terhadap sumbu rotasi. Semakin jauh massa benda dari sumbu rotasi, semakin besar momen inersia dan semakin sulit benda tersebut untuk dipercepat atau diperlambat dalam rotasi.

Rumus umum momen inersia untuk suatu benda adalah:
$$ I = \sum{m_i \cdot r_i^2} $$

Di mana:

• \( I \) adalah momen inersia (dalam kilogram-meter kuadrat atau kg·m²),
• \( m_i \) adalah massa setiap partikel benda,
• \( r \) adalah jarak setiap partikel benda dari sumbu rotasi.

Untuk benda-benda dengan bentuk yang teratur, terdapat rumus khusus untuk menghitung momen inersia, tergantung pada bentuk dan sumbu rotasi. Beberapa rumus momen inersia yang umum adalah:

• Batang panjang dengan sumbu rotasi di tengah: \( I = \frac{1}{12} mL^2 \)
• Silinder atau cakram berotasi pada pusat: \( I = \frac{1}{2} mR^2 \)
• Bola pejal: \( I = \frac{2}{5} mR^2 \)

Contoh Soal Momen Inersia

Soal 1: Sebuah batang homogen dengan panjang 4 meter dan massa 3 kg berotasi pada sumbu yang terletak di tengah batang. Hitung momen inersia batang tersebut.

Penyelesaian:
Diketahui:

• Panjang batang, \( L = 4 \, \text{m} \)
• Massa batang, \( m = 3 \, \text{kg} \)

Rumus momen inersia untuk batang yang berotasi di sumbu tengahnya adalah:
$$ I = \frac{1}{12} mL^2 $$

Maka:
$$ I = \frac{1}{12} \cdot 3 \cdot (4)^2 = 4 \, \text{kg·m}^2 $$

Jadi, momen inersia batang tersebut adalah 4 kg·m².

Soal 2: Sebuah cakram homogen dengan jari-jari 0,5 meter dan massa 2 kg berputar pada sumbu pusatnya. Hitung momen inersia cakram tersebut.

Penyelesaian:
Diketahui:

• Jari-jari cakram, \( R = 0,5 \, \text{m} \)
• Massa cakram, \( m = 2 \, \text{kg} \)

Rumus momen inersia untuk cakram yang berotasi pada sumbu pusatnya adalah:
$$ I = \frac{1}{2} mR^2 $$

Maka:
$$ I = \frac{1}{2} \cdot 2 \cdot (0,5)^2 = 0,25 \, \text{kg·m}^2 $$

Jadi, momen inersia cakram tersebut adalah 0,25 kg·m².

Kesimpulan

Gerak rotasi merupakan bagian penting dalam fisika yang menggambarkan rotasi benda di sekitar sumbu tertentu. Momen gaya atau torsi adalah gaya yang menyebabkan benda berotasi, sedangkan momen inersia adalah ukuran resistansi benda terhadap perubahan dalam gerakan rotasi.

Pemahaman tentang momen gaya dan momen inersia sangat penting dalam menganalisis gerakan rotasi berbagai objek dalam kehidupan sehari-hari, seperti roda kendaraan, kipas angin, atau benda-benda astronomi seperti planet dan bintang.

Melalui rumus-rumus dan contoh soal yang disajikan, kita dapat melihat bagaimana kedua konsep ini bekerja dalam menentukan karakteristik gerak rotasi suatu benda. Dengan latihan yang konsisten, pemahaman terhadap konsep-konsep ini akan semakin mendalam.