Materi Gerak Melingkar Beraturan – Pengertian dan Besarannya

Gerak Melingkar Beraturan (GMB) adalah gerak suatu benda pada lintasan lingkaran dengan kecepatan yang berubah-ubah selalu tegak lurus dengan percepatan. Namun pada fenomena GMB meskipun kecepatannya berubah, lajunya tetap konstan.

Artikel ini akan membahas secara mendalam tentang pengertian Gerak Melingkar, contoh gerak melingkar, dan besaran pada gerak melingkar.

Pengertian Gerak Melingkar Beraturan

Gerak melingkar beraturan adalah gerak pada lintasan melingkar dengan kecepatan tetap dan arah kecepatannya tegak lurus terhadap arah percepatan.

Arah kecepatannya terus berubah seiring dengan gerak benda dalam lingkaran. Karena percepatan didefinisikan sebagai besarnya perubahan kecepatan, maka perubahan arah kecepatan akan mengakibatkan percepatan dan juga perubahan besaran kecepatan.

Oleh karena itu, sebuah benda yang bergerak mengelilingi lingkaran terus mengalami percepatan meskipun kecepatannya tetap \((v_1 = v_2 = v)\).

• Benda yang bergerak melingkar memiliki kecepatan sudut \(\omega\). Semakin besar kecepatan sudutnya, maka benda akan mengalami percepatan sudut \(\alpha\). Karenanya, percepatan sudut \(\alpha\) didefinisikan sebagai perubahan kecepatan sudut tiap satuan waktu.
• Sebuah benda dapat dikatakan bergerak melingkar jika lintasan yang dilewatinya berbentuk lingkaran.
• Gerak melingkar beraturan (GMB) terjadi jika kecepatan anguler benda bernilai tetap (konstan). Persamaan dalam GMB adalah:
  $$\omega = \text{konstan}$$
  $$\theta = \theta_0 + \omega t$$

Posisi Benda pada Gerak Melingkar Beraturan

Jari-jari (r) adalah jarak titik partikel terhadap pusat lingkaran atau pusat rotasi yang besarnya tetap.

Posisi partikel yang sedang bergerak melingkar dapat dinyatakan dengan koordinat polar yaitu representasi antara jari-jari dan sudut sebagai berikut:
$$ \vec{r} = f(r, \theta) $$
Dimana:

• \(vec{r}\) = posisi partikel yang sedang melakukan gerak melingkar (meter, radian)
• \(r\) = jari-jari yaitu jarak titik partikel terhadap pusat lingkaran (meter)
• \(theta\) = sudut yang ditempuh partikel saat itu (radian)

Posisi partikel juga dapat dinyatakan dengan fungsi sudut terhadap waktu disebut Posisi sudut, yaitu:
$$ \theta(t) = \omega t $$
Dimana:

• \(\theta(t)\) = besar sudut tempuh benda (rad)
• \(\omega\) = nilai kecepatan sudut (rad/s)
• \(t\) waktu tempuh benda (s)

Panjang lintasan benda yang bergerak melingkar dapat ditentukan dengan mengalikan besar sudut tempuh \(\theta\) dengan jari-jari lingkaran, yaitu:
$$S = \theta r$$
Dimana:

• \(S\) = panjang lintasan benda (m)
• \(\theta\) = sudut tempuh benda (rad)
• \(r\) = jari-jari lingkaran (m)

Contoh Gerak Melingkar Beraturan

Contohnya salah satunya adalah gerak jarum jam bergerak melingkar dengan kecepatan tetap, tanpa percepatan atau bahkan berhenti secara tiba-tiba, karena perjalanan waktu adalah konstan, yaitu konstan dari hari ke hari. Sehari ada 24 jam, satu jam ada 60 menit, dan satu menit ada 60 detik.

Contoh lainnya yaitu gerak yang terjadi pada bianglala dan komedi putar. Biasanya bianglala dan komidi putar bergerak dengan kecepatan konstan, sehingga memerlukan waktu yang sama antara satu sesi dengan sesi berikutnya.

Selain itu, kecepatan gerak bianglala dan komidi putar sengaja dijaga agar tetap konstan untuk menghindari bahaya yang mungkin timbul.

Besaran dan Rumus pada Gerak Melingkar Beraturan

Kecepatan

Kecepatan dalam gerak melingkar terdiri dari 2 macam yaitu kecepatan sudut \(\vec{\omega}\) dan kecepatan linier \(v)\. Kecepatan sudut dan kecepatan linier memiliki hubungan:
$$v = \vec{\omega} r \Rightarrow \vec{\omega} = \frac{v}{r}$$
Dimana:

• \(vec{\omega}\) = kecepatan sudut (rad/s)
• \(v\) = kecepatan linier (m/s)
• \(r\) = jari-jari lingkaran (m)

Kecepatan sudut sesaat

Kecepatan sudut sesaat (\(\vec{\omega}\)) diperoleh dari turunan posisi sudut terhadap waktu, yaitu:
$$\vec{\omega} = \frac{d\theta}{dt}$$

Dalam gerak melingkar beraturan, kecepatan sudut benda tetap (nilai dan arahnya tetap) maka baik kecepatan sesaat maupun rata-ratanya akan bernilai sama. Sedangkan untuk kecepatan linier, nilainya tetap tetapi arahnya selalu berubah.

Kecepatan sudut ini sering disebut juga frekuensi sudut karena dapat diperoleh dari frekuensi, yaitu:
$$ \omega = 2\pi f = \frac{2\pi}{T} \text{ rad/s} $$

Kecepatan yang diberikan kepada benda ketika bergerak melingkar dalam arah tangensial disebut kecepatan linear.

Keceparan anguler

Kecepatan anguler adalah perubahan sudut dalam selang waktu tertentu. Hubungan kecepatan linear dan kecepatan anguler dapat dituliskan sebagai berikut:
$$v = \omega r$$

Percepatan

Percepatan adalah perubahan kecepatan setiap selang waktu. Untuk melihat apakah ada percepatan dalam gerak melingkar, khususnya gerak melingkar beraturan, mari kita lihat vektor kecepatan sudut dan vektor kecepatan liniernya.

Vektor kecepatan sudut (\(\vec{\omega}\)) memiliki dua komponen yaitu nilai dan arah.

Perubahan nilai (\(\vec{\omega}\)) akan menimbulkan percepatan sudut (\(\vec{\alpha}\)) dan dalam hal ini tidak ada perubahan arah (\(\vec{\omega}\)) karena benda hanya berputar ke satu arah saja, tidak bolak-balik secara cepat dan terus-menerus.

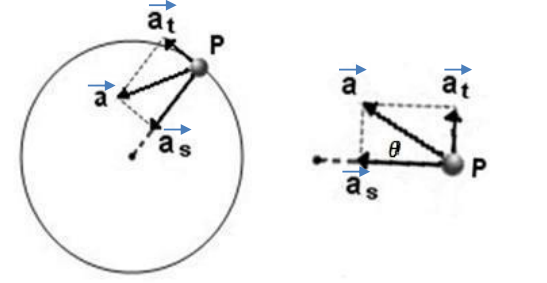
Begitu pula vektor kecepatan linier (\(v\)) mempunyai dua komponen yaitu nilai dan arah. Perubahan nilai $$v$$ akan menimbulkan percepatan tangensial (\(\vec{a_T}\)) dan perubahan arah \(v\) akan menimbulkan percepatan sentripetal (\(\vec{a_s}\)).

Periode dan Frekuensi

Periode adalah waktu yang diperlukan untuk berputar satu putaran penuh. Sedangkan frekuensi adalah banyaknya putaran yang ditempuh oleh suatu benda selama 1 detik/sekon.