Frekuensi Resonansi Rangkaian RLC: Pembahasan, Rumus, dan Contohnya

Frekuensi resonansi merupakan fenomena penting dalam dunia elektronik dengan berbagai aplikasi dalam teknologi modern. Salah satu jenis rangkaian yang memperlihatkan fenomena ini adalah rangkaian RLC.

Rangkaian RLC

Rangkaian RLC adalah rangkaian listrik yang terdiri dari tiga komponen dasar: resistor (R), induktor (L), dan kapasitor (C). Ketiga komponen ini dapat disusun dalam berbagai konfigurasi, baik seri maupun paralel, masing-masing dengan karakteristik unik yang mempengaruhi perilaku rangkaian secara keseluruhan.

1. Resistor (R): Resistor menghambat aliran arus listrik dalam rangkaian. Hambatannya diukur dalam satuan ohm (Ω). Resistor tidak menyimpan energi, melainkan mengubah energi listrik menjadi energi panas.
2. Induktor (L): Induktor menyimpan energi dalam bentuk medan magnet ketika arus listrik mengalir melaluinya. Induktansi, diukur dalam satuan henry (H), menunjukkan kemampuan induktor untuk menyimpan energi ini. Induktor menentang perubahan arus, memberikan impedansi terhadap perubahan arus yang bersifat sementara.
3. Kapasitor (C): Kapasitor menyimpan energi dalam bentuk medan listrik antara dua pelat konduktif yang dipisahkan oleh bahan dielektrik. Kapasitansi, diukur dalam satuan farad (F), menunjukkan kemampuan kapasitor untuk menyimpan muatan listrik. Kapasitor menentang perubahan tegangan di dalam rangkaian.

Jenis Rangkaian RLC

1. Rangkaian RLC Seri: Dalam rangkaian ini, resistor, induktor, dan kapasitor dihubungkan berurutan sehingga arus yang sama mengalir melalui ketiga komponen. Rangkaian ini menunjukkan resonansi pada frekuensi tertentu, di mana impedansi total rangkaian menjadi minimum.
2. Rangkaian RLC Paralel: Dalam rangkaian ini, resistor, induktor, dan kapasitor dihubungkan secara paralel sehingga tegangan yang sama melintasi ketiga komponen. Pada frekuensi resonansi, arus total dalam rangkaian menjadi maksimum karena impedansi rangkaian minimum.

Frekuensi Resonansi

Frekuensi resonansi adalah kondisi di mana rangkaian RLC memperlihatkan reaksi tertentu yang dapat dimanfaatkan dalam berbagai aplikasi.

Resonansi terjadi ketika impedansi rangkaian mencapai nilai tertentu yang meminimalkan atau memaksimalkan arus atau tegangan, tergantung pada jenis rangkaiannya (seri atau paralel).

Terjadinya Frekuensi Resonansi

Frekuensi resonansi terjadi ketika komponen induktif dan kapasitif dalam rangkaian mencapai keseimbangan sempurna. Dalam kondisi ini, energi yang disimpan dalam induktor dan kapasitor berosilasi bolak-balik tanpa diserap oleh resistor.

Pada frekuensi ini, reaktansi induktif (\( X_L \)) dan reaktansi kapasitif (\( X_C \)) dalam rangkaian saling meniadakan, sehingga hanya tersisa komponen resistif (\(R\)) yang berperan.

Frekuensi resonansi adalah frekuensi di mana rangkaian menunjukkan impedansi minimum (dalam rangkaian seri) atau impedansi maksimum (dalam rangkaian paralel). Ini berarti arus akan mencapai nilai maksimum dalam rangkaian seri, dan tegangan akan mencapai nilai maksimum dalam rangkaian paralel.

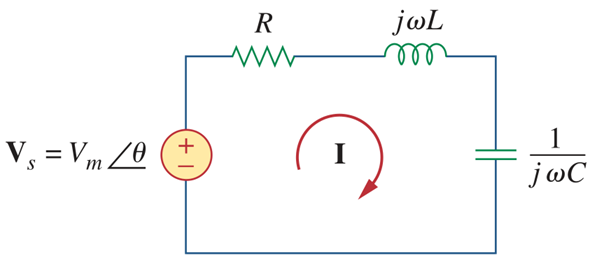
Rumus Frekuensi Resonansi

Frekuensi resonansi dalam rangkaian RLC dihitung menggunakan rumus berikut:
$$ f_r = \frac{1}{2\pi\sqrt{LC}} $$
di mana:

• \( f_r \) adalah frekuensi resonansi (dalam Hertz, Hz),
• \( L \) adalah induktansi (dalam Henry, H),
• \( C \) adalah kapasitansi (dalam Farad, F).

Rumus ini berasal dari fakta bahwa pada frekuensi resonansi, reaktansi induktif (\( X_L \)) sama dengan reaktansi kapasitif (\( X_C \)), sehingga:
$$ X_L = X_C $$
dengan
$$ X_L = 2\pi f L $$
$$ X_C = \frac{1}{2\pi f C} $$

Dengan menyamakan kedua reaktansi ini dan memecahkan untuk frekuensi \( f \), kita mendapatkan rumus frekuensi resonansi di atas.

Penerapan Frekuensi Resonansi dalam Kehidupan Sehari-Hari

Frekuensi resonansi memiliki berbagai aplikasi penting dalam dunia teknik dan teknologi. Beberapa penerapannya adalah:

1. Radio dan Telekomunikasi: Dalam teknologi radio dan telekomunikasi, frekuensi resonansi digunakan untuk memilih frekuensi tertentu dari banyak frekuensi yang tersedia. Rangkaian RLC disetel pada frekuensi tertentu, memungkinkan sinyal radio dengan frekuensi tersebut diperkuat sementara sinyal lainnya ditekan. Ini adalah prinsip dasar di balik tuner radio.
2. Filter Frekuensi: Rangkaian RLC digunakan dalam filter frekuensi untuk memisahkan atau melewati sinyal tertentu dalam rentang frekuensi yang diinginkan. Filter ini digunakan dalam perangkat elektronik seperti equalizer audio, sirkuit pengolahan sinyal, dan peralatan komunikasi.
3. Resonansi Mekanik dan Penginderaan: Fenomena resonansi juga terjadi dalam sistem mekanis. Misalnya, dalam aplikasi penginderaan, resonansi dapat digunakan untuk mendeteksi perubahan kecil dalam lingkungan. Sensor resonansi digunakan dalam deteksi getaran, pengukuran tekanan, dan aplikasi lainnya.
4. Penggunaan dalam Jaringan Listrik: Dalam jaringan listrik, resonansi dapat memiliki dampak positif maupun negatif. Misalnya, resonansi dapat digunakan untuk memperbaiki faktor daya dalam sistem distribusi listrik. Namun, resonansi yang tidak diinginkan juga dapat menyebabkan masalah seperti lonjakan tegangan yang dapat merusak peralatan listrik. Oleh karena itu, penting untuk memahami dan mengendalikan frekuensi resonansi dalam sistem tersebut.

Contoh Soal Frekuensi Resonansi Rangkaian RLC

Contoh Soal 1: Rangkaian RLC Seri

Sebuah rangkaian RLC seri terdiri dari sebuah resistor dengan nilai 50 ohm, sebuah induktor dengan induktansi 0,2 H, dan sebuah kapasitor dengan kapasitansi 100 µF. Hitung frekuensi resonansi dari rangkaian tersebut.

Penyelesaian:
Diketahui:

• Resistor \( R = 50 \, \Omega \)
• Induktor \( L = 0{,}2 \, \text{H} \)
• Kapasitor \( C = 100 \, \mu\text{F} = 10^{-4} \, \text{F} \)

Frekuensi resonansi (\( f_r \)) dapat dihitung menggunakan rumus:
$$f_r = \frac{1}{2\pi\sqrt{LC}} = \frac{1}{2\pi\sqrt{(0{,}2)(10^{-4})}} = 35{,}6 \, \text{Hz}$$

Frekuensi resonansi dari rangkaian tersebut adalah sekitar 35,6 Hz.

Contoh Soal 2: Rangkaian RLC Paralel

Sebuah rangkaian RLC paralel terdiri dari sebuah induktor dengan induktansi 0,5 H, dan sebuah kapasitor dengan kapasitansi 250 µF. Hitung frekuensi resonansi rangkaian tersebut.

Penyelesaian:
Diketahui:

• Induktor \( L = 0{,}5 \, \text{H} \)
• Kapasitor \( C = 250 \, \mu\text{F} = 250 \times 10^{-6} \, \text{F} \)

Frekuensi resonansi (\( f_r \)) dapat dihitung menggunakan rumus yang sama:
$$f_r = \frac{1}{2\pi\sqrt{LC}} = \frac{1}{2\pi\sqrt{(0{,}5)(250 \times 10^{-6})}} = 14{,}2 \, \text{Hz}$$

Jawaban:
Frekuensi resonansi dari rangkaian tersebut adalah sekitar 14,2 Hz.

Contoh Soal 3: Pengaruh Perubahan Kapasitansi terhadap Frekuensi Resonansi

Sebuah rangkaian RLC seri memiliki induktor dengan induktansi 0,3 H dan kapasitor dengan kapasitansi 50 µF. Jika kapasitansi diubah menjadi 100 µF, bagaimana perubahan frekuensi resonansi?

Penyelesaian:
Frekuensi resonansi awal dengan \( C_1 = 50 \, \mu\text{F} \):
$$ f_r = \frac{1}{2\pi\sqrt{LC}} = \frac{1}{2\pi\sqrt{(0{,}3)(50 \times 10^{-6})}} = 41{,}1 \, \text{Hz} $$

Frekuensi resonansi setelah kapasitansi diubah menjadi \( C_2 = 100 \, \mu\text{F} \):
$$f_r = \frac{1}{2\pi\sqrt{LC}} = \frac{1}{2\pi\sqrt{(0{,}3)(100 \times 10^{-6})}} = 29{,}1 \, \text{Hz}$$

Frekuensi resonansi menurun dari 41,1 Hz menjadi 29,1 Hz ketika kapasitansi diubah dari 50 µF menjadi 100 µF.

Contoh Soal 4: Frekuensi Resonansi pada Perubahan Induktansi

Sebuah rangkaian RLC seri memiliki resistor dengan nilai 100 ohm, induktor dengan induktansi 0,1 H, dan kapasitor dengan kapasitansi 20 µF. Jika induktansi berubah menjadi 0,05 H, berapa frekuensi resonansi baru?

Penyelesaian:
Frekuensi resonansi awal dengan \( L_1 = 0{,}1 \, \text{H} \):
$$ f_r = \frac{1}{2\pi\sqrt{LC}} = \frac{1}{2\pi\sqrt{(0{,}1)(20 \times 10^{-6})}} = 112{,}5 \, \text{Hz} $$

Frekuensi resonansi setelah induktansi diubah menjadi \( L_2 = 0{,}05 \, \text{H} \):
$$f_r = \frac{1}{2\pi\sqrt{LC}} = \frac{1}{2\pi\sqrt{(0{,}05)(20 \times 10^{-6})}} = 159{,}2 \, \text{Hz}$$

Jawaban:
Frekuensi resonansi meningkat dari 112,5 Hz menjadi 159,2 Hz ketika induktansi berubah dari 0,1 H menjadi 0,05 H.

Referensi:

• Sarah, L. L., dan Suwarna, I.R. 2022. Fisika untuk SMA/MA Kelas XII, Jakarta Pusat: Pusat Kurikulum dan Perbukuan Kementrian Pendidikan, Kebudayaan, Riset, dan Teknologi.
• Roboguru.ruangguru.com. Frekuensi resonansi suatu rangkaian seri RLC
• Ruangguru.com. Penjelasan Rangkaian Seri RLC pada arus bolak-balik
• Quipper.com. Inilah Rangkaian RLC Beserta Contoh Soalnya
• Ilustrasi oleh Unsplash.com